UVa 294: Divisors
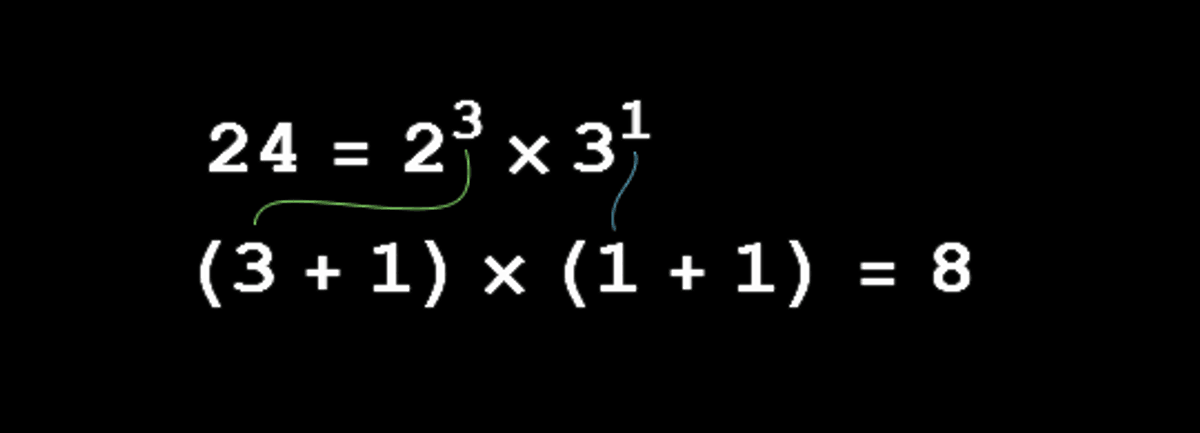
— Competitive Programming, Solutions — 8 min read
In UVa 294, Divisors, we are asked to find the number with the maximum number of divisors in a given range. Counting number of divisors is a classic problem, and there exists a fast and simple way to do it. We start off with a straight-forward, but slow, implementation and progressively optimize it until it’s fast enough. We don’t stop there, though, but we end with a much faster implementation by noticing that divisor count is related to prime factorization.
Read the problem description here.
Interpretation
The problem description is straight-forward and easy to understand, but there are some things we must note before moving forward, that is, and can be as big as and their difference can be as big as . The numbers are too big for a simple-minded approach to work (as said in the problem description), so we have to find a fast algorithm to avoid getting a Time Limit Exceeded verdict from the online judge. Also note that if two or more numbers all have the maximum divisor count, then the smallest one should be selected.
Implementation
We’ll start off by implementing the main method. We loop from $L$ to $U$ and compute the divisor count, making use of the divisorCount function that we have yet to implement, and keep track of the number with the highest divisor count. Then we output the result in the format described in the problem description.
public static void main(String[] args) throws Exception { Scanner in = new Scanner(System.in); PrintWriter out = new PrintWriter(System.out, true);
int tests = in.nextInt(); // read the number of tests
// for each test for (int test = 0; test < tests; test++) {
int L = in.nextInt(), // read L U = in.nextInt(), // read U maxDivisorCount = 0, // the maximum divisor count found maxNumber = 0; // the number with the maximum divisor count
// loop through the numbers for (int i = L; i <= U; i++) {
// the divisor count of the current number // the divisorCount function calculates it for us int currentDivisorCount = divisorCount(i);
// if the current divisor count is larger than // the largest divisor count (a contradiction), // then the current divisor count is the // largest divisor count if (currentDivisorCount > maxDivisorCount) {
// update appropriate variables maxDivisorCount = currentDivisorCount; maxNumber = i; } }
// output the result in the correct format out.printf("Between %d and %d, %d has a maximum of %d divisors.\n", L, U, maxNumber, maxDivisorCount); }}Now we just have to implement the divisorCount function.
Our first attempt at the divisorCount function will be to loop through all numbers from $1$ to $n$ and count how many of them are divisors of $n$.
public static int divisorCount(int n) { // a counter for the number of divisors int count = 0;
// loop through 1..n for (int i = 1; i <= n; i++) if (n % i == 0) // if the remainder of n divided by i is 0 count++; // then i is a divisor of n
// return the number of divisors return count;}This method tests $n$ numbers, which is bad. We can do way better…
It’s easy to see that $n$ is always a divisor of $n$, and that the second-biggest divisor is at most $n/2$. We can use that fact to cut our search space in half. Now we can modify our divisorCount function to only check numbers from $1$ to $n/2$.
public static int divisorCount(int n) { // a counter for the number of divisors // intially 1 because n is a divisor of n int count = 1;
// loop through 1..n/2 for (int i = 1; i <= n / 2; i++) if (n % i == 0) // if the remainder of n divided by i is 0 count++; // then i is a divisor of n
// return the number of divisors return count;}Now we are only checking $n/2$ numbers, but we can still do one more (but big) optimization to our current method.
Now, let’s say that $n = 12$. Its divisors are $1,2,3,4,6,12$. If we split the list into two, $1,2,3$ and $4,6,12$, we see that for each number $k$ in the left list, $n/k$ is in the right list. For example, $2$ is in the left list and $12/2 = 6$ is in the right list. Now we only have to look for numbers in the left list, and for each number we find in that list we increment our divisor counter by $2$, not by $1$, because of the corresponding divisor in the right list. But where does the left list stop, and the right list start? Well, that’s exactly $\sqrt{n}$. So in other words, for every divisor below the square root, there exists exactly one divisor above the square root. The only exceptions are square numbers, but we need to be careful not to count their square root twice, since it will be in both lists.
Now we’ll only loop from $1$ to $\sqrt{n}$, and count each divisor we find twice.
public static int divisorCount(int n) { if (n == 1) // 1 is a tricky number, return 1; // so we'll handle it separately
// a counter for the number of divisors int count = 0;
// save the square root to avoid re-computation int sqrt = (int)Math.sqrt(n);
// loop through 1..sqrt(n) for (int i = 1; i <= sqrt; i++) if (n % i == 0) // if the remainder of n divided by i is 0 count += 2; // then i and n/i are divisors of n
// if n is a square number, then // we counted sqrt(n) twice if (sqrt * sqrt == n) count--; // so we fix the count
// return the number of divisors return count;}Now we’re only checking $\sqrt{n}$ numbers, and that is about as good as it gets using this kind of brute-force algorithm to compute the divisor count. Our solution is currently fast enough to get an Accepted verdict, but we can still do better.
Divisor Count through Prime Factorization
We won’t be able to optimize our current algorithm more, so if we want a faster solution, we are going to have to think of a better way than checking each number.
Once again, let’s assume $n = 12$. We all know how to find the prime factors (aka. the prime factorization) of a number (and if not, take a look at Wikipedia), and since we’re trying to find some patterns, we might as well factorize $12$. The prime factorization of $12$ is $2^2 \times 3$. Now that we’ve factorized $12$, we might as well factorize its divisors (smiley-face).
$$ \begin{array}{|c|c|} \hline \text{Divisor} & \text{Factorization} \\ \hline 1 & 1 \\ \hline 2 & 2 \\ \hline 3 & 3 \\ \hline 4 & 2^2 \\ \hline 6 & 2 \times 3 \\ \hline 12 & 2^2 \times 3 \\ \hline \end{array} $$
Now notice that the divisors have very similar prime factorizations to $12$. More precisely, they just have different combinations of the powers of the primes. The powers of $2$ range from $0$ to $2$ (same as the power of $2$ in $12$), and the powers of $3$ range from $0$ to $1$ (same as the power of $3$ in $12$). Now if we were to count the divisors of $12$, we would use combinatorics and get $(2+1)(1+1)$. Or more generally for any number $n = p_1^{a_1} p_2^{a_2} \cdots p_k^{a_k}$, where $p_i$ is the $i$-th prime factor and $a_i$ is the power of that prime factor, its divisor count is $(a_1+1)(a_2+1)\cdots(a_k+1)$.
Our new algorithm finds the prime factorization of the number, and then computes the divisor count according to our new formula. Note that I use an optimized trial division, similar to what we did above, to find the prime factorization, but we could also have used a list of primes.
public static int divisorCount(int n) { // a counter for the number of divisors // intially 1 (the multiplication identity) int count = 1;
// save the square root to avoid re-computation int sqrt = (int)Math.sqrt(n);
// loop through 2 and the odd numbers up to sqrt(n) for (int i = 2; i <= sqrt; i = (i == 2 ? 3 : i + 2)) {
// a counter for the power of the // current number in the prime factorization int pow = 0;
// while i is in n's prime factorization while (n % i == 0) { pow++; // increment the power count n /= i; // remove one i from the prime factorization of n }
// if there were any i's in n's prime factorization if (pow != 0) { // change the divisor count according to our formula count *= pow + 1;
// recompute the square root, since we've changed n // (a little optimization) sqrt = (int)Math.sqrt(n); } }
// if we've still not removed all factors from n, // then there is one prime factor left if (n != 1) // change the divisor count according to our formula // (the power of the last prime is 1) count *= 1 + 1;
// return the number of divisors return count;}Conclusion
We started with a very slow trial division algorithm, but after some optimizations and some mathematical thinking, we realized that divisor count is related to prime factorization, and used that insight to develop a way faster algorithm. Our current solution is more than fast enough to get an Accepted verdict at the online judge.
If you still want more about divisor count and prime factorization, you might want to take a look at Project Euler 12 and Project Euler 12 – Revisited.
You can take a look at the complete source code here.
So what do you think? Did/would you solve it differently? Let me know in the comments.